Section: New Results
Plasma physics
Analysis of the drift approximation
Participants : Hervé Guillard, Afeintou Sangam, Philippe Ghendrih [IRFM, CEA Cadarache] , Yanick Sarazin [IRFM, CEA Cadarache] , Patrick Tamain [IRFM, CEA Cadarache] .
Drift approximation consider the slow evolution of the fields in the vicinity of a tokamak equilibrium. These models are typically used to study the micro-instabilities that are believed to be responsible of turbulent transport in tokamaks. Since the drift asymptotic uses a “slow” scaling of the velocity field, the resulting models are significantly different from the full MDH models. This is particularly true with respect to the computation of the electric field that is given by an Ohm's law in MHD models whereas it is computed by a vorticity-like evolution equation in drift approximations. Drift asymptotic models are extremely interesting from a computational point of view since they save substantial CPU time and computer memory. However, the mathematical and numerical properties of these models are essentially unknown. We have begun a detailed study of the derivation of these models from two-fluid Braginskii-type models in order to establish the range of applicability of these asymptotic models, understand their mathematical properties and relations with the reduced MHD models and design appropriate numerical methods for their approximations.
Stabilized C1-Finite Element Method for MHD
Participants : Boniface Nkonga, Marie Martin.
Reduced MHD models are often used in plasma physics and therefore fast compressible waves are not taken into account. In the context of Elms instabilities investigations, full and extended MHD models are to be considered within the framework of high order finite element approximation. In order to obtain predictive simulations with reduced, full and extended MHD models, it is crucial to design numerical strategies that can face some difficulties related to the use of the classical Galerkin methods for convection dominated flows. We have developed a general VMS stabilization strategy for time dependent implicit scheme, which can be applied to MHD models in order to preserved the global accuracy of the initial Galerkin formulation and enforce physical properties as monotony and positivity. Higher order of continuity shape functions are important for accuracy and also help to obtain more robustness of the stabilization as there is no more singularities on elements edges. Numerical implementation and preliminary validations has been performed using C1-Bell shapes functions for triangular meshes. Order five accuracy of the theory is recovered for specific boundary condition. Improvement for general boundary condition is still an open issue. The next step is to combine this Bell shapes functions in the poloidal direction with B-splines functions to achieve accurate representation of complex torus as ITER.
Two fluid modelling of the Scrape-Off-Layer Plasma
Participants : Audrey Bonnement, Hervé Guillard, Richard Pasquetti.
A two fluid physical model has been developped in close collaboration with researchers from IRFM. It is based on an hypothesis of stationary magnetic field and the electrostatic and electroneutrality assumptions. However the usual drift assumption, e.g. used in the CEA code TOKAM3D (thesis of P. Tamain), is not used. On the basis of the conservation equations of density, electron and ion velocities, electron and ion temperatures and electrical charges, a set of 10 nonlinear coupled partial differential equations (PDE) can be set up. Our investigations rely on the development of two solvers for this set of PDE. In the frame of her thesis, A. Bonnement (co-direction H. Guillard and R. Pasquetti, financial support of INRIA and PACA region, industrial partner ASSYSTEM) uses a Finite volume / element (FV/FE) approach. The other code, developed by R. Pasquetti, focuses on the use of high order approximations: a spectral element method (SEM) is used in the poloidal plane whereas Fourier expansions are used in the toroidal direction. Each of these codes has allowed in 2010 to solve strongly anisotropic diffusion equations in 2D and axisymmetric 3D geometries for the FV/FE code and in 2D and fully 3D for the Fourier-SEM code. The FV/FE code has also been used to carry out a study of radiative layers evolution in a 2D annular configuration but also in a realistic 3D ITER configuration.
Works carried out during the year 2011 are described hereafter: – On the basis of a Godunov scheme, the FV/FEd approach has been extended to solve the axisymmetric Euler, Navier-Stokes or Braginskii like systems in the jet-tokamak geometry. With respect to Navier-Stokes, the Braginskii system is characterized by anisotropies in the transport coefficients. The mesh is unstructured : A finite element approximation is used for the diffusion terms whereas for the convective terms a finite volume approximation is used on the dual mesh. We have especially focused on the treatment of the toroidal geometry. We have also focused on the implementation of the so-called Bohm conditions, which are enforced by imposing that at the limiter the fluid velocity is colinear to the magnetic field and that the « parallel Mach number » equals or is greater than one. In these studies the governing equations are completed by constant force terms in order to model the Lorentz forces as well as sources of mass and energy. Such forcing terms allow to preserve an equilibrium state, e.g. obtained on the basis of simulations that make use of the drift assumption (see next paragraph). We have then introduced perturbations of this equilibrium state to study the evolution of the different variables (density, velocity and temperature). Various perturbations have been used to this end, fully random in order to check the stability of the equilibrium or on the contrary localized, in order to roughly model the injection of pellets inside the SOL. It is planned that Audrey Bonnement will defend her thesis in Spring 2012.
The SEM-Fourier 3D code has been extended to solve the full set of governing equations. The unknowns are then the density, the velocity of the center of mass, the electric current and potential, the ion and electron internal energies. In time, this set of PDE is solved by using an IMEX (Implicit – Explicit) approach, based on the combination of an explicit Runge-Kutta scheme for the flux terms and on a DIRK (diagonal implicit Runge Kutta) for the Lorentz terms, which indeed lead to an unconditionnaly unstable scheme if treated explicitly. A projection method is used to enforce the divergence free constraint of the current, so that an additional solve of a Poisson equation is required to obtain the potential. The Bohm conditions are here implemented by enforcing that the ion pressure is such that the parallel Mach number shows the expected value, i.e. equal or greater than one. The main difficulty that we presently meet is that the initial condition that we use does not correspond to an equilibrium state, so that instabilities quickly develop till yielding an unsteady flow not consistent at the limiter with the Bohm condition. Detailed analyses of these results are presently carried out with Sebastian Minjeaud (new CNRS researcher of the LJAD) to provide relevant explanations of the observed phenomena.
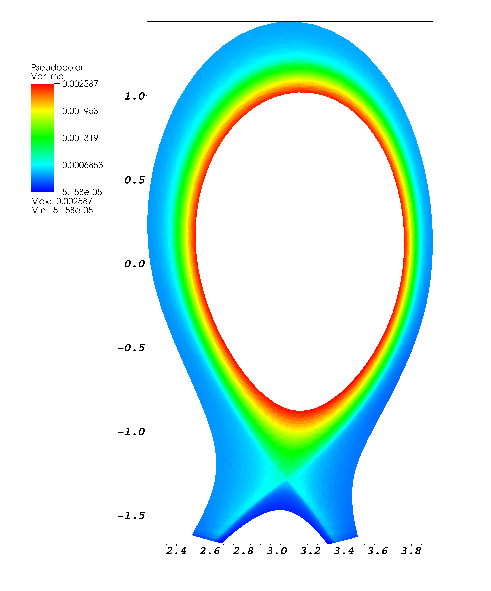
Drift approximation modelling of the Scrape-Off-Layer Plasma
Participants : Marco Bilanceri, Hervé Guillard.
Based on a fluid model using the drift velocity approximation, a simulation method have been designed to compute the flow in the scrape-off-layer of a Tokamak. The variables used by the model are the particle number, the parallel (to the magnetic field) velocity and the electric potential. The spatial approximation uses a finite volume/finite element approach and is therefore easy to apply to complex geometries. Bohms boundary conditions are used on the divertor plates of the machine. The figure 1. shows the density in a poloidal cut where the influence of the separatrix can be clearly seen.